Abstract:
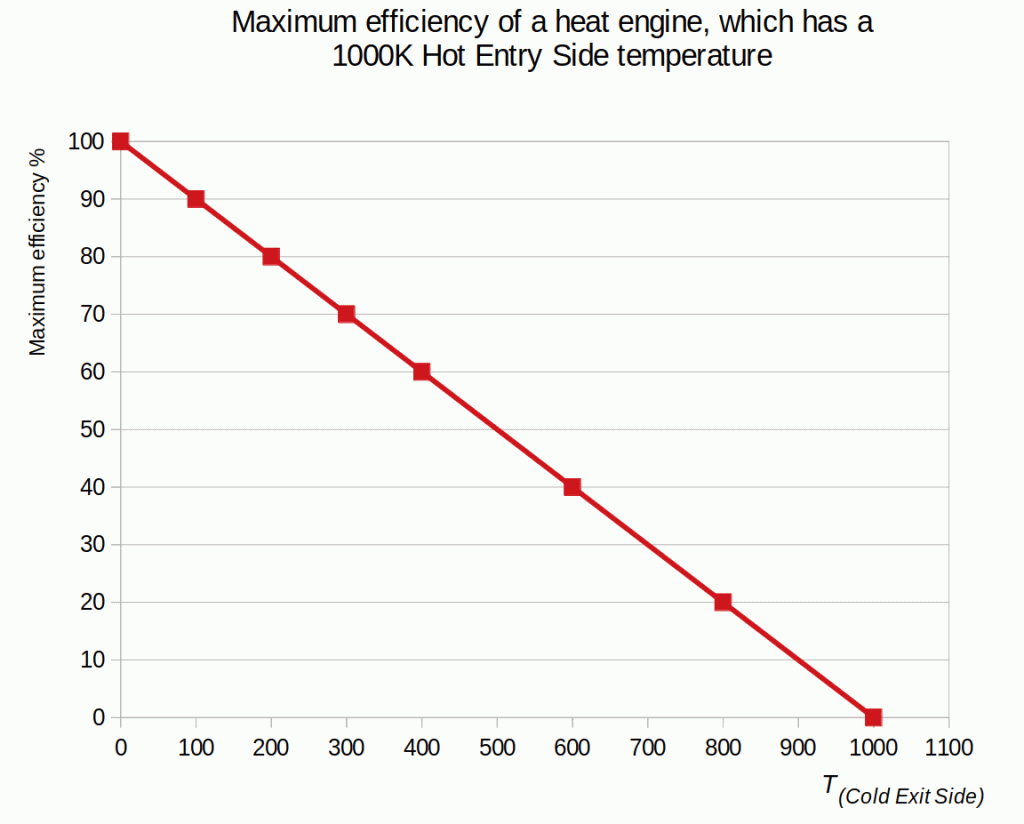
The gas laws bind together volume, pressure and temperature. Despite that, Sadi Carnot discovered in 1824 that only the heat engine’s hot- and cold-side temperatures determine its maximum efficiency. Since then, the engineers have been calculating efficiencies using temperatures and an equation:
Ƞmax = ȠCarnot = 1 – T(cold reservoir) / T(hot reservoir)
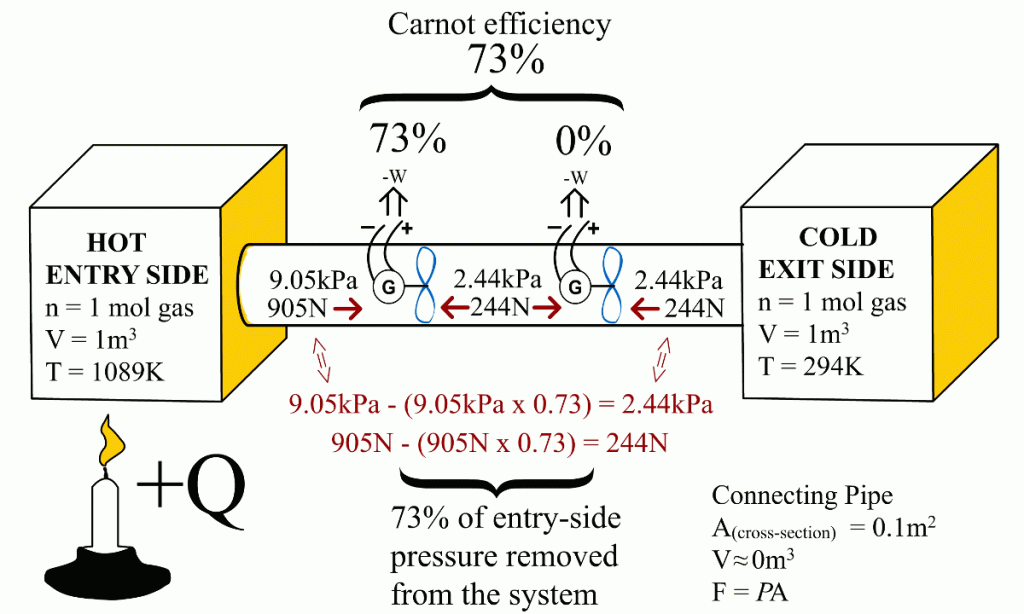
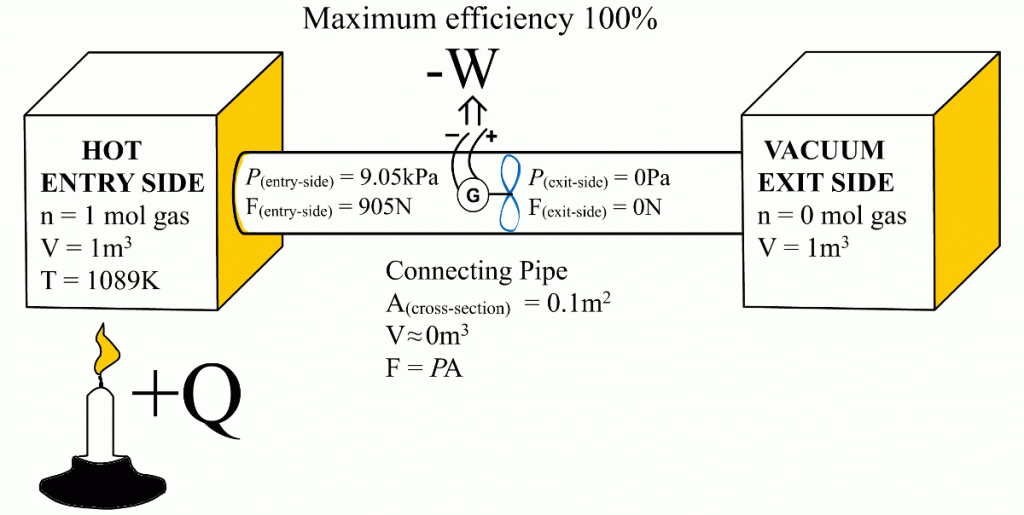
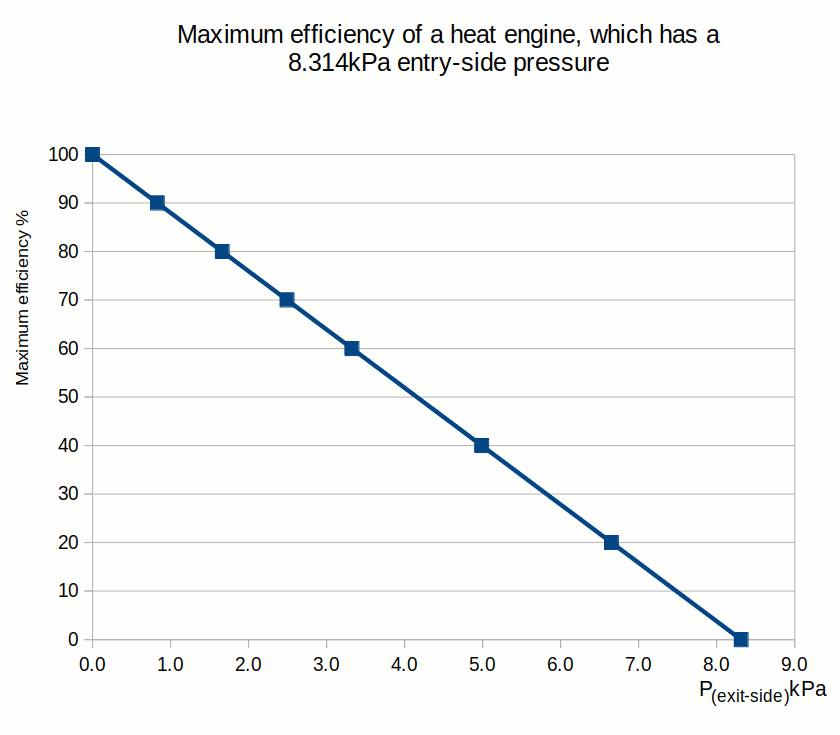
This article shows that the same Carnot efficiency values can be obtained using the exit- and entry-side pressures. Also, the more universal equation for calculating maximum efficiencies for heat engines is:Ƞmax = 1 - P(exit-side) / P(entry-side)
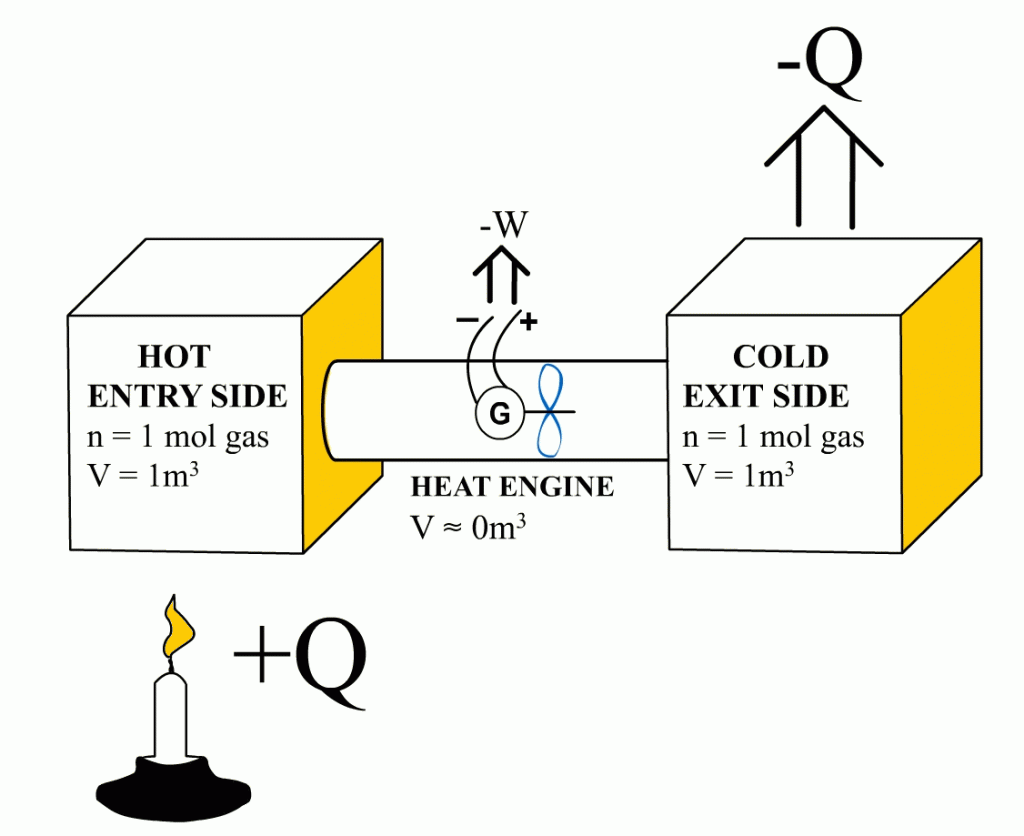
This article demonstrates that it is the entry-side’s relative over-pressure that is powering the heat engines. When the Carnot efficiency’s share of energy has been removed from the system, the pressure coming from the entry-side has been reduced to an equal level with the exit-side pressure. At that moment, the exit-side’s pressure pushes the heat engine with equal force from the opposite direction than the entry-side’s pressure is pushing it. Ultimately, these equal but opposite forces end the heat engine’s ability to obtain energy with a higher efficiency from the system – precisely at that Carnot efficiency level. The functional role of the exit-side pressure is to reduce the heat engine’s ability to remove heat energy from the system in form of useful work. This article also links together the Newton’s laws of motion and the engine efficiency.