Sadi Carnot discovered that a heat engine’s hot and cold side temperature determines its maximum efficiency. Therefore, since 1824 engineers have been measuring heat engine’s hot and cold side temperatures and quite successfully determining each heat engine’s achieved and expected maximum efficiency. Carnot’s theorem has an error because it ignores the impact of having different pressures at the heat engine’s entry and exit sides. This error doesn’t show an error in results when the heat engine operates in an environment where its entry and exit sides are connected to the same and unlimited external pressure source. But when the pressure difference exits, the heat engine’s efficiency does not obey the usual equation used for calculating the heat engine’s efficiency.
Ƞmax = ȠCarnot = 1 - T(cold-side) / T(hot-side)
Instead, the efficiency can and should be calculated using the heat engines’ entry and exit side
pressures as follows…
Ƞmax = 1 - P(exit-side) / P(entry-side)
Evidence 1: Same Carnot efficiency values can be obtained using the entry and exit side temperatures OR pressures
Next, I’ll prove that it is the pressures that determine the heat engine’s efficiency. First, I’ll show that the entry and exit side pressures can be used to obtain the same Carnot efficiency values obtained using the hot-side and cold-side temperatures. This demonstration uses the following closed heat engine system: two containers with known volumes and a known amount of ideal gas substance. Both of these containers are attached to the heat engine’s entry and exit sides. In addition, we assume the heat engine itself to be volumeless or having an insignificantly small volume in comparison to the volume of the entry and exit side containers.
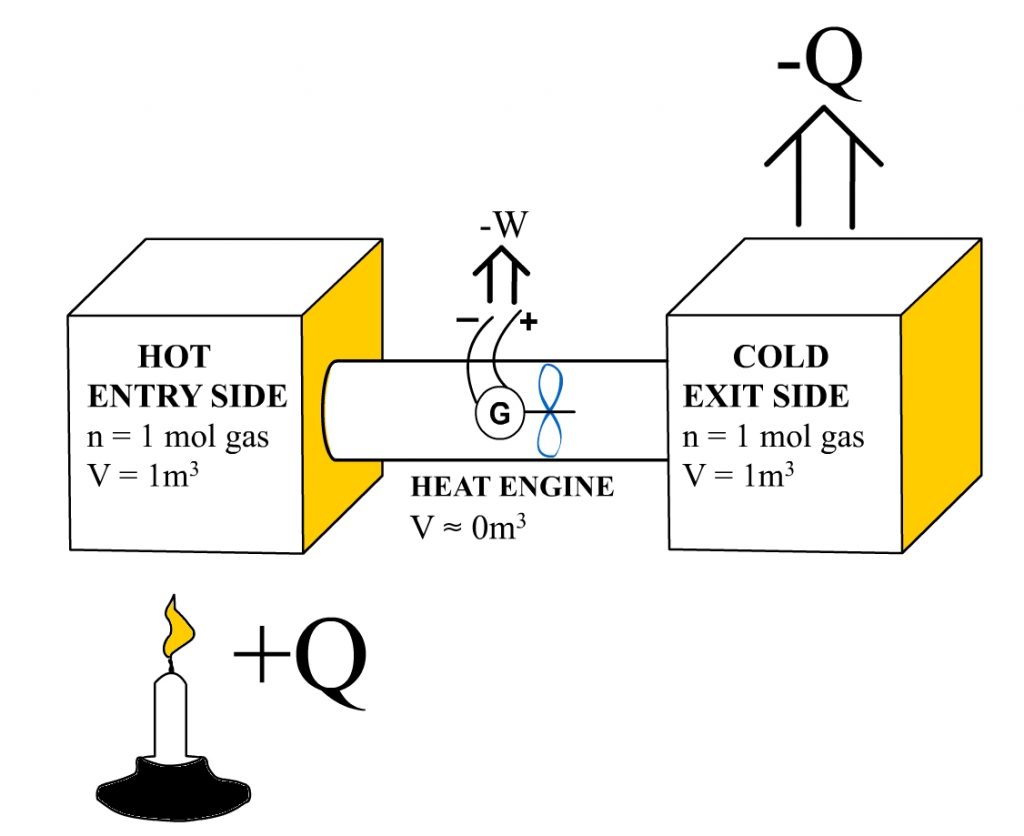
Let’s assume that the “Hot Entry Side” was initially heated to 1089K, while the Cold Exit Side remained at 294K. At this point, the pressure inside the “Hot Entry Side” can be calculated to be 9054.45Pa, and the pressure inside the “Cold Exit Side” can be calculated to be 2444.45Pa. A handy Online calculator can be used in making those calculations.
| Carnot efficiency value obtained from the hot entry side and cold exit side temperatures | Same efficiency value obtained from the Hot Entry Side and Cold Exit Side pressures |
Ƞ(Carnot) = 1 –T(cold-side)/T(hot-side) ==> Ƞ(Carnot) = 1 – 294K/1089K==> Ƞ(Carnot) = 73.003% | Ƞalternative = 1 – P(exit)/P(entry)==> Ƞalternative = 1 – 2444.45Pa/9054.45Pa==> Ƞalternative = 73.003% |
Table 1: Same Carnot efficiency values can be obtained using the entry and exit side temperatures or pressures
To prove that this was not just a coincidence, we use different entry and exit side temperatures.
| Entry-side container temperature (K) | Exit-side container temperature (K) | entry-side container pressure (kPa) | Exit-side container pressure (kPa) | ȠCarnot (1-TCold/THot) x 100% | Ƞalternative (1-Pexit/Pentry) x 100% |
| 300 | 300 | 2.49434 | 2.49434 | 0.00% | 0.00% |
| 301 | 300 | 2.50265 | 2.49434 | 0.33% | 0.33% |
| 400 | 300 | 3.32579 | 2.49434 | 25.00% | 25.00% |
| 450 | 300 | 3.74151 | 2.49434 | 33.33% | 33.33% |
| 500 | 300 | 4.15723 | 2.49434 | 40.00% | 40.00% |
| 600 | 300 | 4.98868 | 2.49434 | 50.00% | 50.00% |
| 700 | 300 | 5.82012 | 2.49434 | 57.14% | 57.14% |
| 800 | 300 | 6.65157 | 2.49434 | 62.50% | 62.50% |
| 900 | 300 | 7.48302 | 2.49434 | 66.67% | 66.67% |
| 1000 | 300 | 8.31446 | 2.49434 | 70.00% | 70.00% |
| 1089 | 294 | 9.05445 | 2.44445 | 73.00% | 73.00% |
| 1000 | 1 | 8.31446 | 0.008314 | 99.90% | 99.90% |
| 1000 | 0 | 8.31446 | 0.00000 | 100.00% | 100.00% |
Table 2: Maximum Carnot efficiency values can be calculated from various entry Vs. exit side pressures
The results in table 2 show the systematic correlation between the Entry Vs. Exit side temperatures and pressures.
Evidence 2: Heat engine’s maximum efficiency percentage is equal to its entry side over-pressure percentage
The pressure difference between its entry and exit sides determines the heat engine’s ability to perform external work. The values shown in table 1 demonstrate that when the temperatures or pressures at the heat engine’s entry and exit sides are the same, the heat engine’s maximum efficiency is 0%. Thus, it cannot do any external work. Table 2 also shows that if additional heat (or pressure) is added to the heat engine’s entry side, the heat engine obtains the ability to produce external work.
When any heat engine does some external work, it always takes its host system’s internal energy. That lost internal energy manifests itself in the form of the fluid’s reduced temperature and pressure. Next, we show that the over-pressure at its entry side limits the heat engine’s maximum efficiency when that over-pressure has been consumed, adding successive heat engines for the purpose of harvesting more of the remaining heat is a pointless.
In this demonstration, an almost similar device arrangement can be used as was used earlier with evidence1. The difference this time is that we have two independent heat engines placed inside that pipe that connects the “Hot Entry Side” and “Cold Exit Side.” Picture 2 show this arrangement. In picture 2, we initially assume that the Hot Entry Side has been heated to 1089K, causing the 1mol of ideal gas inside the 1m3 container to obtain a pressure of 9054.45Pa. Similarly, we assume that the “Cold Exit Side” container with 1 mol of an ideal gas and a volume of 1m3 will obtain a 2444.45Pa pressure. Earlier, the Carnot efficiency for this kind of system was calculated to be 0.73003.
Ƞ(Carnot) = 1 –T(cold-side)/T(hot-side)
==> Ƞ(Carnot) = 1 – 294K/1089K x100%
==> Ƞ(Carnot) = 73.003%
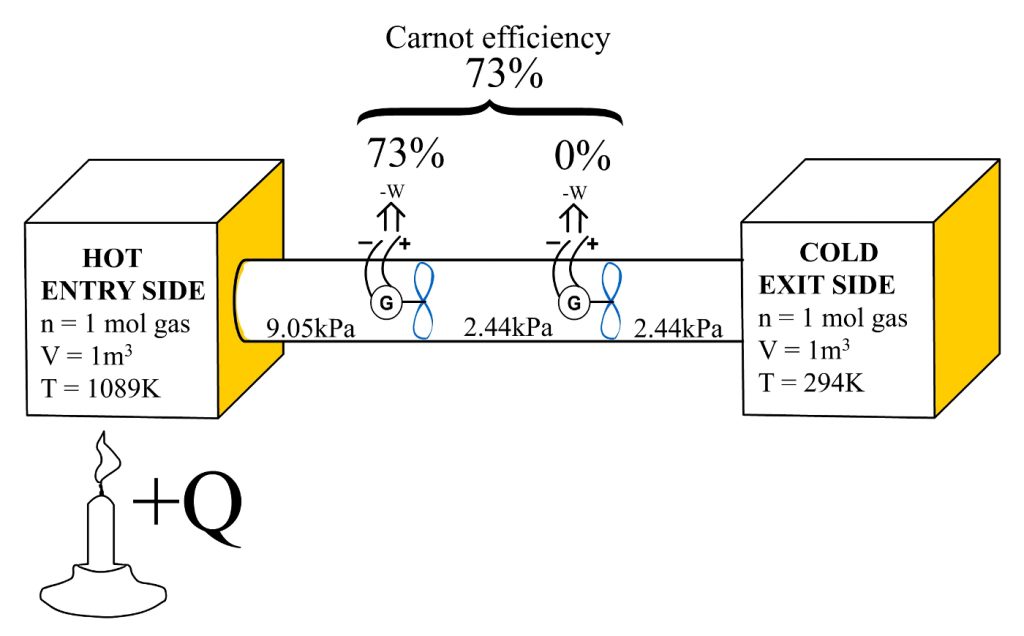
Picture 2: The reduction entry side pressure by the Carnot efficiency percentage, is equal to the exit side pressure level
Lets see what happens to the entry side pressure if we remove 73.003% of it ?
9054.45Pa – ((9054.45Pa / 100) x 73.003) = 2444.43Pa
What a coincidence! When we reduce the Hot Entry Side pressure by Carnot efficiency share of pressure, the remaining “Hot Entry Side” pressure equals to Cold Exit Side pressure; 2444.43Pa Vs. 2444.45Pa. Furthermore, we can also obtain the Carnot efficiency value by calculating…
Ƞ2nd alternative-method = (Pentry – Pexit) / Pentry
Ƞ2nd alternative-method = (9054.45Pa – 2444.43Pa) / 9054.43Pa
Ƞ2nd alternative-method = 0.73003
To ensure this is not a coincidence, we did similar calculations to different Hot Entry Side Vs. Cold Exit Side temperature/pressure combinations. The results of those are shown in table 3.
| Entry-side container temperature (K) | Exit-side container temperature (K) | entry-side container pressure (kPa) | Exit-side container pressure (kPa) | (Pentry – Pexit) / Pentry x 100% | Carnot efficiency % |
| 300 | 300 | 2.49434 | 2.49434 | 0.00% | 0.00% |
| 301 | 300 | 2.50265 | 2.49434 | 0.33% | 0.33% |
| 400 | 300 | 3.32579 | 2.49434 | 25.00% | 25.00% |
| 450 | 300 | 3.74151 | 2.49434 | 33.33% | 33.33% |
| 500 | 300 | 4.15723 | 2.49434 | 40.00% | 40.00% |
| 600 | 300 | 4.98868 | 2.49434 | 50.00% | 50.00% |
| 700 | 300 | 5.82012 | 2.49434 | 57.14% | 57.14% |
| 800 | 300 | 6.65157 | 2.49434 | 62.50% | 62.50% |
| 900 | 300 | 7.48302 | 2.49434 | 66.67% | 66.67% |
| 1000 | 300 | 8.31446 | 2.49434 | 70.00% | 70.00% |
| 1089 | 294 | 9.05445 | 2.44445 | 73.00% | 73.00% |
| 1000 | 1 | 8.31446 | 0.008314 | 99.90% | 99.90% |
| 1000 | 0 | 8.31446 | 0.00000 | 100.00% | 100.00% |
Table 3: Carnot efficiency can also be obtained by calculating (Pentry – Pexit) / Pentry
The results in table 3 show the deterministic role of the exit side pressure to the overall available efficiency of the system. The results in table 3 indicate that the Carnot efficiency is limited by the”Cold Exit Side” pressure and predictable. Also, when the Carnot efficiency worth of heat has been removed from the entry side, its pressure equals the “Cold Exit Side” pressure.
Conclusions
Picture 2 and Table 3 indicate that the “Hot Entry Side” pressure cannot be reduced more than the Carnot efficiency percentage. For example, if the left side heat engine, that is shown in picture 2, could operate with a thermal efficiency of 74%, it would cause the “Cold Exit Side” container to have a higher pressure than is the pressure between those two heat engines; causing the molecules from the “Cold Exit Side” to flow towards the area between those heat engines. As shown in tables 2 and 3, the heat engine’s efficiency is zero when the entry side pressure equals exit side pressure. It was also demonstrated that when the entry side pressure is reduced by a percentage equal to the Carnot efficiency, that reduced pressure level will be the pressure level that exists at the “Cold Exit Side.”
Only logical explanation for these effects is that
- All heat engines are powered by the pressure difference between their entry and exit sides.
- A heat engine cannot reduce the fluid’s pressure to a lower pressure level than is found at the “Cold Exit Side”.
- The pressure at the “Cold Exit Side” reduces the thermal efficiency which the heat engine can achieve; by pushing back and opposing the flow of the molecules coming from the Hot Entry Side.
- If the “Cold Exit Side” exhibits no pressure, the heat engine can operate with up to 100% efficiency
- The Carnot’s equation for calculating the maximum efficiency of heat engines should be replaced with an equation Ƞmax = 1 – P(exit-side) / P(entry-side)
- When the heat engine has consumed all the heat derived pressure, the heat engine may continue to operate if there is additional source of pressure; according to Dalton’s law all the partial pressures add up.
Juuso Hukkanen (24.8.2021)
and some hashes… sha256:c7f25e5813e3adaea060438f7e5acfd9b9c5e56a9942ceaf69a15d880503aa30
sha1:a3288c78958b35dea35978b92b494901b256772f
md5:6c334a5915eca82ff38053d3a6e7e39d